Whenever people start talking about NP-Complete problems, or even NP problems, one of the first examples they reach for is the classic Traveling Salesperson Problem. TSP makes sense because it intuitively can’t be solved quickly due to how difficult the problem sounds, so it’s reasonable for people to use it in discussions about P versus NP.
The problem is, 99% of the time people discuss Traveling Salesperson being NP-Complete, they are wrong. The Traveling Salesperson Problem, as it is usually described, isn’t NP-Complete at all. In fact, it’s not even in NP.
The Traveling Salesperson Problem is typically described as “given a graph of cities various distances away from each other, find the shortest path for a salesperson to visit every city exactly once and return to the origin city.”
More formally, TSP is “Given a graph \(G\) of vertices \(V\) connected via nonzero cost edges \(E\), find the lowest-cost Hamiltonian circuit”

Traveling Salesperson from Wolfram Mathworld
However, this particular version of the problem is the optimization problem (“find the lowest cost”). There is another version of the problem, the decision problem, which is “Given a graph \(G\) and a cost \(k\), decide if there is a Hamiltonian circuit whose cost \(\le k\).”
The decision problem, the one which requires a cost to be given and simply decides if there is a cheaper (or equal) Hamiltonian circuit, is NP-Complete. But almost everyone who talks about “the Traveling Salesperson Problem” is talking about the optimization problem, which is not NP-Complete, it is NP-Hard.
What does it mean for a problem to be in NP? It’s actually simpler than it is often made out to be: A problem is in NP if, given a correct answer (a certificate) to that problem, you could verify that it is correct on a deterministic turing machine, in polynomial time.
That’s it. Some might object to this definition, wondering “doesn’t the algorithm that solves the problem have to run in \(O(2^n)\) or some other terrible runtime?” In fact, no. Every problem in P is also in NP since P is a subset of NP. Every problem in P has a deterministic, polynomial-time verifier - they must, since they have polynomial time deciders! Having a polynomial-time verifier is necessary and sufficient for a problem to be in NP.
So what’s NP-Hard? A problem is NP-Hard if every problem in NP can be reduced to it, meaning it is at least as hard or harder than any problem in NP.
A problem is NP-Complete if and only if it is both in NP-Hard and NP.
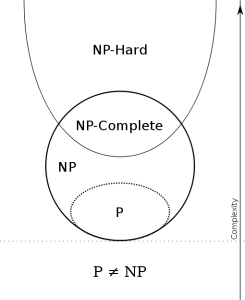
Complexity Classes (assuming P != NP)
The traveling salesperson decision problem has a polynomial-time deterministic verifier. Given a connected graph \(G\) and a cost \(k\) and a candidate (a cycle that hits every vertex and costs less than or equal to \(k\)) \(C\), we can quickly verify that \(C\) has the same number of vertices as \(G\) and that its cost is less than or equal to \(k\). Therefore, the decision version of the problem, TSP-DECIDE, is in NP. And since it’s also in NP-Hard, TSP-DECIDE is NP-Complete.
But we do not have any known polynomial-time verifier for the optimization version of the problem, TSP-OPTIMIZE. If you were given a path, how would you verify that it truly is the lowest-possible cost without checking all other possible Hamiltonian cycles and making sure none of them cost less? Is it possible that TSP-OPTIMIZE is also NP, and therefore NP-Complete? Yes, it has not been proven that there cannot be a polynomial-time deterministic verifier for TSP-OPTIMIZE, though it certainly seems unlikely there would be one. But as it stands, TSP-OPTIMIZE is not in NP because it lacks the verifier, so it is in NP-Hard but not NP-Complete.
TL;DR: For now TSP-OPTIMIZE is in NP-Hard but not (necessarily) in NP, so its not in NP-Complete. TSP-DECIDE is both in NP-Hard as well as NP, and is therefore NP-Complete.
Mistakenly referring to the optimization version of Traveling Salesperson as NP-Complete is unbelievably common among computer science students, so common that I took it for granted that it was the case for years. I just saw this article in Communications of the ACM which refers to:
The NP-complete traveling salesperson problem asks for the smallest distance tour through a set of specified cities.
So next time a computer science person tells you that Traveling Salesperson is NP-Complete, ask them to define what they mean by “Traveling Salesperson”, you’ll be surprised how often they will say “lowest cost” and get it wrong. And hopefully, if you’ve been getting it wrong for years, you’ll now know better.
UPDATE: This post has been linked to by Hacker News and Reddit now, so lots of knowledgable people have begun leaving enlightening comments. Please read them as well, they explain some things that I was not entirely clear about.